Overview
The objective of this project is to take digitized images from Prokudin-Gorskii's glass plate collection and use image processing techniques to automatically create a color image with minimal visual artifacts. To achieve this, I needed to extract the three individual color channels (red, green, and blue) from each image, layer them on top of each other, and align them to form a single RGB image.
I started with a single-scale implementation to align the color channels in low-resolution images. For larger, high-resolution images, I used a multi-scale image pyramid approach to ensure efficient and accurate alignment. This method helped manage the larger file sizes while maintaining speed and precision.



Approach
Brute Force
In the brute force approach, I split the image into three equal parts corresponding to the blue, green, and red color channels. The goal was to align the green and red channels with the blue channel by trying various shifts in the x and y directions.
However, this method didn’t always align the images properly, especially for larger or more complex images. This brute force apporach wasn’t precise enough, resulting in misaligned color channels and noticeable visual artifacts. As seen in the image below, the channels didn’t line up correctly, producing a blurred and offset effect that negatively impacted the quality of the final color image. A more advanced and efficient alignment method was needed.

SDD vs NCC
I explored two different methods for aligning the color channels: Sum of Squared Differences (SSD) and Normalized Cross-Correlation (NCC).
During the alignment process, I encountered cases where the dimensions of the images were slightly different. To address this, I cropped the larger image to match the size of the smaller one. While this method ensures that the images can be compared directly, the downside is that we are losing some portions of the image data. However, the regions being cropped often consist of irrelevant information, such as borders or misaligned areas, which wouldn’t significantly affect the final result. I also added a timing feauture to see how long it took to run the program to compare the processing time for SSD and NCC.
Sum of Squared Differences (SSD):
This method measures the difference between pixel intensities of two images and squares the result to penalize larger discrepancies. The SSD for two images I1 and I2 and is calculated as
SSD = Σ(l1(x, y) - l2(x, y))2
The alignment with the lowest SSD score indicates the best match. Since SSD is straightforward and computationally less expensive, it runs faster, making it a suitable choice for aligning images, especially when speed is critical. For example, the processing time for SSD took 0.19 seconds, which is 57.78% faster than NCC's processsing time.

Normalized Cross-Correlation (NCC):
NCC compares the similarity between two images by normalizing their pixel intensities, which helps account for brightness differences. The NCC for images l1 and l2 is calculated as
NCC = (Σ(l1(x, y) - ̄l1)(l2(x, y) - ̄l2)) / √(Σ(l1(x, y) - ̄l1)2 Σ(l2(x, y) - ̄l2)2)
While NCC is more robust, especially for images with varying lighting conditions, it is computationally more expensive due to the normalization process. This made it slower to run, particularly on larger images. For example, the processing time for NCC took 0.45 seconds, which is 136.84% slower than SDD.

Multi-scale Pyramid
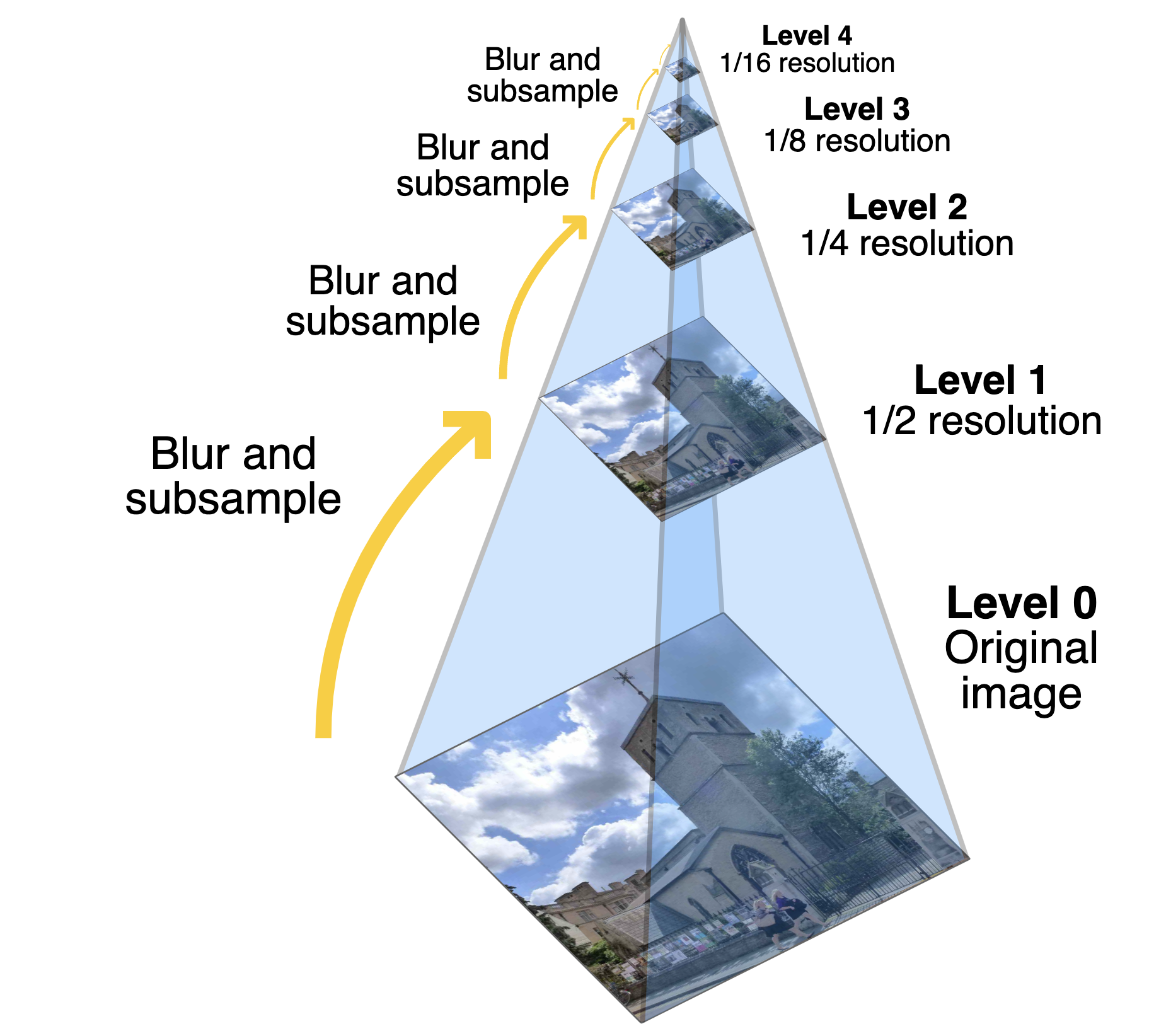
The multi-scale pyramid algorithm is for aligning two images using a coarse-to-fine strategy. The purpose of this approach is to handle large image alignments more efficiently by progressively aligning lower-resolution versions of the images first and then refining the alignment at higher resolutions. The code begins by recursively downscaling the images using a scale_factor, which generates progressively smaller versions of the images. At each level of the image pyramid, the algorithm computes a shift using the smaller versions and scales this shift back to the original resolution. The sdd_align function is then used to fine-tune the alignment at each level, ensuring precise alignment with minimal computational cost. This pyramid approach avoids the need for an exhaustive search at the full resolution, making it faster while still achieving accurate results. Finally, the combined shifts from all levels are applied to the original image to align it with the reference image. This method is particularly useful for large images, where aligning at full resolution in one pass would be computationally expensive and error-prone.
Results
Below is an example of the output:













