Overview
In this project, I will explore image processing techniques focused on filters and frequency analysis. I'll start by applying 2D convolutions to detect edges using finite difference operators and Gaussian filters, followed by creating sharpened images using unsharp masking. Then, I’ll create hybrid images by blending the high and low frequencies of different images, allowing them to change in interpretation based on viewing distance. Finally, I will implement multiresolution blending using Gaussian and Laplacian stacks to seamlessly merge two images, such as blending an apple and an orange. Throughout, I'll experiment with different filters and techniques to gain a deeper understanding of image manipulation.
Part 1: Fun with Filters




The main difference between the original finite difference and the DoG method is the level of noise to find the edges. The finite difference operator tends to highlight not only the true edges but also the noise in the image, especially in regions with small intensity variations, when applied without any smoothing. This often leads to a noisy edge detection. The DoG method first applies Gaussian smoothing to the image, which effectively reduces noise before detecting edges. This makes the edges much cleaner and more distinct, with less false edges caused by noise.
The results obtained using the Derivative of Gaussian filters are very similar to those obtained through the two-step approach of applying Gaussian smoothing with finite difference operators. The reason for this is that the Derivative of Gaussian filters combine both smoothing and differentiation into a single operation. This approach achieves the same objective of reducing noise and detecting edges in a single convolution.
Part 2: Fun with Frequencies!
Image "Sharpening"
Progression of the original image to the sharpened image






Hybrid Images
Fourier analysis in hybrid images helps visualize the distribution of different frequency components, which affects how we perceive the image. Low-frequency components represent smooth variations and broad features, visible when the image is viewed from a distance. High-frequency components capture fine details and edges, dominating perception when viewed up close. By applying low-pass and high-pass filters to two images, you can blend their frequency content, creating a hybrid image that changes interpretation based on viewing distance. Fourier analysis reveals how the frequencies from both images combine, showing the balance between low and high-frequency content in the final hybrid image.
Cat and Derek




Old and Yound




Spiderman and Peter Parker




Multi-resolution Blending
I implemented both Gaussian and Laplacian stacks from scratch, without using any built-in pyramid functions. The Gaussian stack was created by applying a Gaussian filter iteratively at each level without downsampling, resulting in images that retain the original dimensions across all levels. The Laplacian stack was generated by subtracting consecutive levels of the Gaussian stack, capturing the high-frequency components of the image at each level.

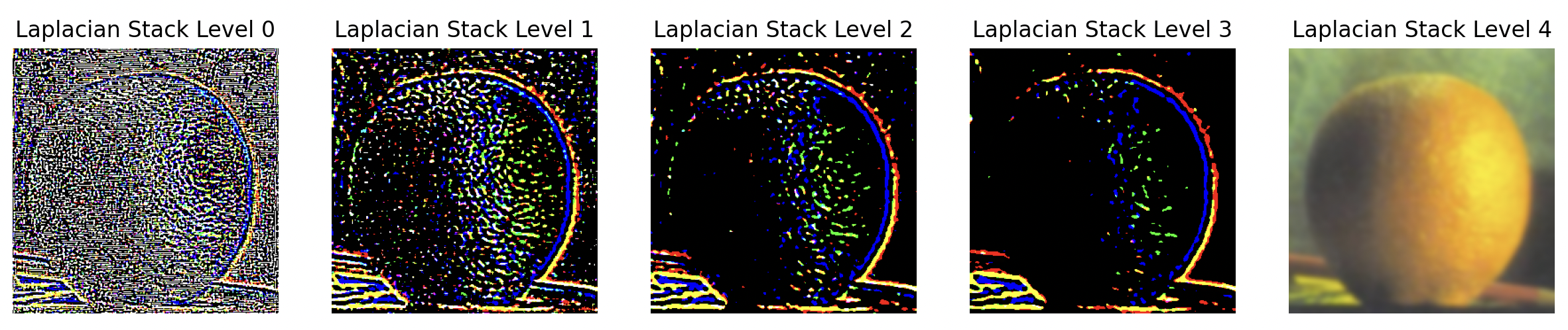
Blending
Orapple



Soccer ball and Baseball



Irregular Blending


